ЗЂВМепЃКжаЙЋШэПМ РДдДЃКжаЙЋШэПМ 2021-05-08 09:51:11 ![]() дФЖС()
дФЖС()
ЪдЬт1 (15ЗжЃЌУППе3Зж)
дФЖСЯТСаЫЕУїКЭСїГЬЭМЃЌНЋгІЬюШы(n) ЕФзжОфаД дкД№ЬтжНЕФЖдгІРИФкЁЃ
СїГЬЭМЫЕУї
ЯТУцЕФСїГЬЭМУшЪіСЫЖд8ЮЛЖўНјжЦећЪ§ЧѓВЙЕФЫуЗЈЁЃ
ИУЫуЗЈЕФМЦЫуЙ§ГЬШчЯТЃКДгЖўНјжЦЪ§ЕФЕЭЮЛ(зюгвЮЛ)ПЊЪМЃЌвРДЮЯђИпЮЛж№ЮЛВщПДЃЌжБЕНЪзДЮгіЕН“1”ЪБЃЌЭЃжЙВщПДЁЃШЛКѓЃЌЖдИУ“1”ЮЛзѓУцЕФИќИпЮЛ(ШчЙћгаЕФЛА)ЃЌж№ЮЛЧѓЗДЃЌЫљЕУЕФНсЙћОЭЪЧЖддЖўНјжЦЪ§ЧѓВЙЕФНсЙћЁЃ
Р§ШчЃКЖдЖўНјжЦећЪ§10101000ЧѓВЙЕФНсЙћЪЧ01011000ЁЃ
Щш8ЮЛЖўНјжЦећЪ§жаЕФИїЮЛЃЌДгЕЭЮЛЕНИпЮЛЃЌвРДЮДцЗХдкећаЭЪ§зщBITЕФBIT[1]~BIT[8]жаЁЃР§ШчЃЌЖўНјжЦећЪ§10101000ДцЗХдкЪ§зщBITКѓЃЌОЭгаBIT[1]=0,BIT[2]=0,...,BIT[7]=0, BIT[8]=1ЁЃ ШєСїГЬЭМжаДцдкПеВйзїЃЌдђгУNOPБэЪОЁЃ
СїГЬЭМ
СїГЬЭМжа(1) ДІАД “бЛЗБфСПУћЃКбЛЗГѕжЕЃЌдіСПЃЌбЛЗжежЕ”ИёЪНУшЪіЁЃ
ЪдЬт1ЗжЮі
БОЬтПМВщЕФЪЧСїГЬЭМЁЃ
гЩгкЬтФПжаИјГіСЫЖд8ЮЛЖўНјжЦећЪ§ЧѓВЙЕФЫуЗЈЃЌВЂЧвжИУїНЋ8ЮЛЖўНјжЦећЪ§жаЕФИіЮЛЃЌДгЕЭЮЛЕНИпЮЛЃЌвРДЮДцЗХдкећаЭЪ§зщBITЕФBIT[1]~BIT[8]жаЃЌвђДЫЃЌбЛЗПижЦБфСПЕФГѕжЕгІИУЮЊ1(ДгЖўНјжЦЪ§жаЕФзюЕЭЮЛПЊЪМ)ЁЂжежЕЮЊ8 (ЖўНјжЦЪ§жаЕФУПвЛЮЛЖМвЊМьВщ)ЁЂдіСПЮЊ1(УПДЮМьВщ1ЮЛ)ЃЌАДее“бЛЗБфСПУћЃКбЛЗГѕжЕЃЌдіСПЃЌбЛЗжежЕ”ИёЪНУшЪіЃЌдђЮЊЃКi:lЃЌ1ЃЌ8ЁЃ
гЩЬтФПжаИјГіЕФЫуЗЈПЩжЊЃЌДгзюгвЮЛПЊЪМЯђзѓевЕНЕФЕквЛИі“1”МАЦфгвБпЕФИїЮЛЪЧВЛШЁЗДЕФЃЌвђДЫашвЊвЛИіБъжОЃЌswЦ№ЕФОЭЪЧетИізїгУЁЃ
гЩгкswЕФГѕЪМжЕЮЊ0ЃЌЫљвддкевЕНДггвБпЪ§ЕФЕк1Иі“l”жЎЧАЃЌЕБBIT[i]ЕШгк“0”ЧвswЕШгк0ЃЌдђЫЕУїетаЉЖўНјжЦЮЛЮоашШЁЗДЃЌвђДЫЯргІЕФСїГЬЭМжаПе(4)ДІЕФВйзїгІЮЊПеВйзїЁЃЕБФГИіBIT[i]ЕФжЕЕШгк“1”ЧвswЕФжЕЕШгк0ЃЌдђЫЕУїевЕНСЫДггвБпЪ§ЕФЕк1Иі“l”ЃЌДЫЪБгІНЋswЕФжЕжУЮЊЗЧ“0”ЃЌвђДЫСїГЬЭМжаПе(2)ДІЕФВйзїЮЊswИГжЕЁЃ
зюКѓЃЌгІНЋЦфгрИїЮЛШЁЗДЃЌМДBIT[i]ЕШгк1ЪБЃЌдкСїГЬЭМжаЕФПе(3)ДІНЋЦфИГжЕ0;ЗДжЎЃЌдђдкСїГЬЭМжаЕФПе(5)ДІНЋЦфИГжЕ1ЁЃ
ВЮПМД№АИ
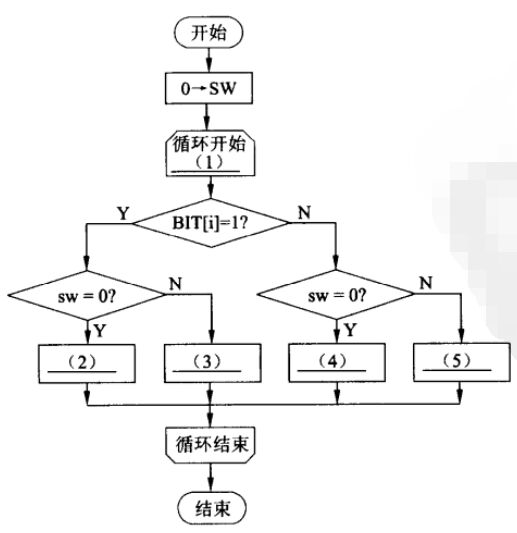
(1) iЃК1ЃЌ1ЃК8
(2) 1→swЃЌ Лђk→swЧвk≠0
(3) 0→BIT[i]
(4) NOPЃЌЛђПеВйзї
(5) 1→BIT[i]

ЗжЯэзюЧАбиаавЕЖЏЬЌЁЂвЕФкЪБЦРЃЌДђдьзЈвЕШэПМНЛСїШІ

БИПМНЛСїЁЂИЩЛѕЙВЯэЃЌбЇЯАИїжжШэПМПМЪдММЧЩ